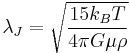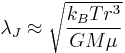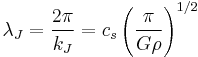Jeans length
Jeans' length is the critical radius of a cloud (typically a cloud of interstellar dust) where thermal energy, which causes the cloud to expand, is counteracted by gravity, which causes the cloud to collapse. It is named after the British astronomer Sir James Jeans, who concerned himself with the stability of spherical nebula in the early 1900s.[1]
The formula for Jeans Length is:
where 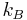 is Boltzmann's constant,
is Boltzmann's constant,  is the temperature of the cloud,
is the temperature of the cloud,  is the radius of the cloud,
is the radius of the cloud,  is the mass per particle in the cloud,
is the mass per particle in the cloud,  is the Gravitational Constant and
is the Gravitational Constant and  is the cloud's mass density (i.e. the cloud's mass divided by the cloud's volume).[1]
is the cloud's mass density (i.e. the cloud's mass divided by the cloud's volume).[1]
Perhaps the easiest way to conceptualize Jeans' Length is in terms of a close approximation, in which we discard the factors 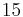 and
and 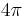 and in which we rephrase
and in which we rephrase  as
as 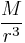 . The formula for Jeans' Length then becomes:
. The formula for Jeans' Length then becomes:
It is then immediately obvious that 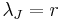 when
when 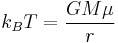 i.e. the cloud's radius is the Jeans' Length when thermal energy per particle equals gravitational work per particle. At this critical length the cloud neither expands nor contracts. It is only when thermal energy is not equal to gravitational work that the cloud either expands and cools or contracts and warms, a process that continues until equilibrium is reached.
i.e. the cloud's radius is the Jeans' Length when thermal energy per particle equals gravitational work per particle. At this critical length the cloud neither expands nor contracts. It is only when thermal energy is not equal to gravitational work that the cloud either expands and cools or contracts and warms, a process that continues until equilibrium is reached.
Jeans' Length as oscillation wavelength
The Jeans' Length is the oscillation wavelength below which stable oscillations rather than gravitational collapse will occur.
Where G is the gravitational constant, 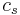 is the sound speed, and
is the sound speed, and  is the enclosed mass density.
is the enclosed mass density.
It is also the distance a sound wave would travel in the collapse time.
References
- ^ "The Stability of a Spherical Nebula". Philosophical Transactions of the Royal Society of London. 1902. JSTOR 90845.
See also
- Langmuir waves (similar waves in a plasma)
- Jeans instability